Урок №9. Миноры и алгебраические дополнения
Миноры матрицы
Пусть дана квадратная матрица А, n - ого порядка. Минором некоторого элемента аij , определителя матрицы n - ого порядка называется определитель (n - 1) - ого порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент аij. Обозначается Мij.
Рассмотрим на примере определителя матрицы 3 - его порядка:
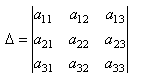
, тогда согласно определению минора, минором М12, соответствующим элементу а12, будет определитель:
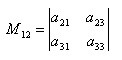
При этом, с помощью миноров можно облегчать задачу вычисления определителя матрицы. Надо разложить определитель матрицы по некоторой строке и тогда определитель будет равен сумме всех элементов этой строки на их миноры. Разложение определителя матрицы 3 - его порядка будет выглядеть так:
 |
|
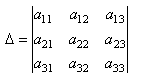, знак перед произведением равен (-1)n, где n = i + j.
Алгебраические дополнения:
Алгебраическим дополнением 
элемента 
определителя называется выражение вида: 
= 
, где 
минор элемента 
.
Тогда можно переформулировать изложенное выше свойство.
Определитель матрицы равен сумме произведений элементов некоторого ряда (строки или столбца) матрицы на соответствующие им алгебраические дополнения.
Пример. Алгебраическое дополнение элемента 
:
= 
= 
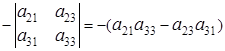
Пример:
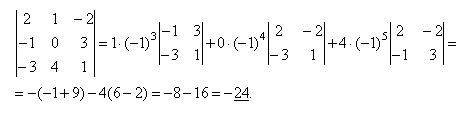
Невырожденная матрица – квадратная матрица, определитель которой не равен нулю.
Вырожденная матрица – квадратная матрица, определитель которой равен 0.
Вычисление определителя
Вычисление определителя может осуществляться путем разложения его по любой строке (столбцу) следующим образом,
по строке: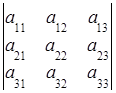 
= 
+
+
, (
=1,2,3);
по столбцу: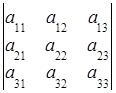 
= 
+
+
, (
=1,2,3).
Пример. Разложение определителя по первой строке
= 
+
+
;
= 
= 
;
= 
= 
;
=
= 
;
=
.
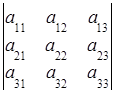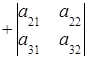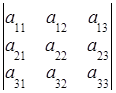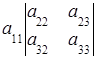
Пример. Вычисление определителя путем разложения по первой строке
= 
= 
;
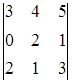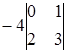
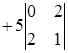Аналогично данный определитель можно разложить по любой другой строке (столбцу).
Обратная матрица
Матрица 
называется обратной матрице 
, если 
= 
= 
, где 
- единичная матрица.
Всякая невырожденная матрица имеет обратную матрицу и притом только одну, т.е. для того чтобы квадратная матрица A имела обратную матрицу, необходимо и достаточно, чтобы её определитель был отличен от нуля.
Для получения обратной матрицы используют формулу:
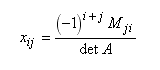
, где Мji дополнительный минор элемента аji матрицы А.
Свойства обратных матриц:
- (А-1)-1 = А;
- (АВ)-1 = В-1А-1;
- (АТ)-1 = (А-1)Т;
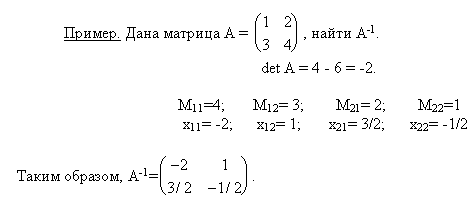
Пример. Для матрицы A найти обратную.
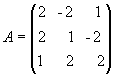
Решение. Находим сначала детерминант матрицы А
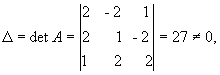
значит, обратная матрица существует.
откуда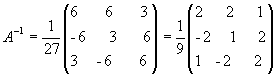 
Составитель: Салий Н.А.