Главная » Уроки по Численным методам » Урок 12. Ранг матрицы. Вычисление ранга матрицы. Норма матриц

Урок №12. Ранг матрицы. Вычисление ранга матрицы. Норма матриц.

Если все миноры матрицы Aпорядка kравны нулю, то все миноры порядка k+1, если такие существуют, тоже равны нулю.
Рангом матрицы A называется наибольший из порядков миноров матрицы A, отличных от нуля.
Максимум ранг может быть равен минимальному числу из количества  строк или столбцов матрицы, т.е. если матрица имеет размер 4х5, то максимум ранг будет 4.
Минимум ранг матрицы равен 1, если только вы не имеете дело с нулевой матрицей, там всегда ранг равен нулю.
        
Ранг невырожденной квадратной матрицы порядка n равен n, так как ее определитель является минором порядка n и у невырожденной матрицы отличен от нуля.  
При транспонировании матрицы ее ранг не меняется.

Пусть ранг матрицы равен $ r$. Тогда любой минор порядка $ r$, отличный от нуля, называется базисным минором.         
Пример. Дана матрица А.
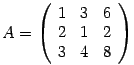
$ {A=\left(\begin{array}{rrr}1&3&6\\ 2&1&2\\ 3&4&8\end{array}\right)}$
Определитель матрицы $ A$ равен нулю.
Минор второго порядка . Следовательно, r(A)=2 и минор базисный.
Базисным минором является также минор .
Минор , т.к. =0, поэтому не будет базисным.
Задание: самостоятельно проверить, какие еще миноры второго порядка будут базисными, а какие нет.         

 

Нахождение ранга матрицы с помощью вычисления всех ее миноров требует слишком большой вычислительной работы. (Читатель может проверить, что в квадратной матрице четвертого порядка 36 миноров второго порядка.) Поэтому для нахождения ранга применяется другой алгоритм. Для его описания потребуется ряд дополнительных сведений.

Назовем элементарными преобразованиями матриц следующие действия над ними:
1) перестановка строк или столбцов;
2) умножение строки или столбца на число отличное от нуля;
3) добавление к одной из строк другой строки, умноженной на число или добавление к одному из столбцов другого столбца, умноженного на число.

        При элементарных преобразованиях ранг матрицы не меняется.
        Алгоритм вычисления ранга матрицы похож на алгоритм вычисления определителя и заключается в том, что с помощью элементарных преобразований матрица приводится к простому виду, для которого найти ранг не представляет труда. Так как при каждом преобразовании ранг не менялся, то, вычислив ранг преобразованной матрицы, мы тем самым находим ранг исходной матрицы.

Пусть требуется вычислить ранг матрицы $ A$ размеров mxn.

  1. С помощью перестановки строк и столбцов матрицы добиваемся того, чтобы в левом верхнем углу матрицы стоял ненулевой элемент. Итак, считаем, что 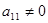. Первую строку оставляем без изменений.
  2. Ко второй строке прибавляем первую, умноженную на число .
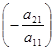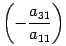  3. К третьей строке прибавляем первую строку, умноженную на число $ \left(-\dfrac{a_{31}}{a_{11}}\right)$.
  4. Процесс продолжаем до тех пор, пока не получим нуль на первом месте в последней строке. В результате получим матрицу А1, в которой в первом столбце все элементы равны 0, кроме элемента .


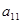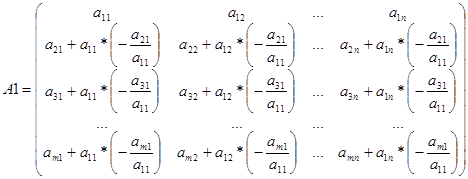
В результате расчетов матрица А1 имеет вид
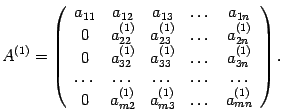
$\displaystyle A^{(1)}=\left(\begin{array}{ccccc}a_{11}&a_{12}&a_{13}&\dots&a_{1... ...ots&\dots\\ 0&a_{m2}^{(1)}&a_{m3}^{(1)}&\dots&a_{mn}^{(1)}\end{array}\right).$

  1. Если все строки, начиная со второй, в полученной матрице нулевые, то ее ранг равен 1, так как есть минор первого порядка, отличный от нуля 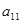. В противном случае перестановкой строк и столбцов матрицы с номерами, большими единицы, добиваемся, чтобы второй элемент второй строки был отличен от нуля. Итак, считаем, что .
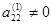  2. Первую и вторую строки оставляем без изменений.
  3. К третьей строке прибавляем вторую, умноженную на число 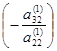. В результате получим, что второй элемент третьей строки равен нулю.
  4. Затем к четвертой строке прибавляем вторую, умноженную на число 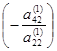, и т.д. В результате получаем матрицу

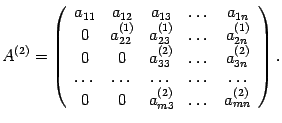
$\displaystyle A^{(2)}=\left(\begin{array}{ccccc}a_{11}&a_{12}&a_{13}&\dots&a_{1... ...ts&\dots&\dots&\dots\\ 0&0&a_{m3}^{(2)}&\dots&a_{mn}^{(2)}\end{array}\right).$
Если все строки, начиная с третьей, нулевые, то , так как минор $ {\left\vert\begin{array}{cc}a_{11}&a_{12}\\ 0&a_{22}^{(1)}\end{array}\right\vert=a_{11}a_{22}^{(1)}\ne0}$. Иначе перестановкой строк и столбцов с номерами, большими двух, добиваемся, чтобы третий элемент третьей строки был отличен от нуля. Далее, добавлением третьей строки, умноженной на соответствующие числа, к строкам с большими номерами получаем нули в третьем столбце, начиная с четвертого элемента, и т.д.
На каком-то этапе мы придем к матрице, у которой все строки, начиная с (r+1)-ой , равны нулю (или отсутствуют при ), а минор в первых $ r$строках и первых $ r$столбцах является определителем треугольной матрицы с ненулевыми элементами на диагонали. Ранг такой матрицы равен $ r$. Следовательно, Rang(A)=r.     
        
В предложенном алгоритме нахождения ранга матрицы все вычисления должны производиться без округлений. Сколь угодно малое изменение хотя бы в одном из элементов промежуточных матриц может привести к тому, что полученный ответ будет отличаться от ранга исходной матрицы на несколько единиц.         
Если в исходной матрице элементы были целыми числами, то и вычисления удобно производить без использования дробей. Поэтому на каждом этапе целесообразно умножать строки на такие числа, чтобы при вычислениях дроби не возникали.         

В лабораторно-практической работе рассмотрим пример нахождения ранга матрицы.

АЛГОРИТМ НАХОЖДЕНИЯ НОРМЫ МАТРИЦЫ.
Выделяют всего три нормы матрицы.
Первая норма матрицы = максимальному из чисел, полученных при сложении всех элементов каждого столбца, взятых по модулю.
Пример: пусть дана матрица А размера 3х2 (рис.10). В первом столбце стоят элементы: 8, 3, 8. Все элементы положительные. Найдем их сумму: 8+3+8=19. Во втором столбце стоят элементы: 8, -2, -8. Два элемента - отрицательные, поэтому при сложении этих чисел, необходимо подставлять модуль этих чисел (т.е. без знаков "минус"). Найдем их сумму: 8+2+8=18. Максимальное из этих двух чисел - это 19. Значит первая норма матрицы равна 19.

Нормы матрицы
Рисунок 10.

Вторая норма матрицы представляет из себя квадратный корень из суммы квадратов всех элементов матрицы. А это значит мы возводим в квадрат все элементы матрицы, затем складываем полученные значения и из результата извлекаем квадратный корень.
В нашем случае, 2 норма матрицы получилась равна квадратному корню из 269. На схеме, я приближенно извлекла квадратный корень из 269 и в результате получила приблизительно около 16,401. Хотя более правильно не извлекать корень.
Норма матрицы

Третья норма матрицы представляет из себя максимальное из чисел, полученных при сложении всех элементов каждой строки, взятых по модулю.
В нашем примере: в первой строке стоят элементы: 8, 8. Все элементы положительные. Найдем их сумму: 8+8=16. В второй строке стоят элементы: 3, -2. Один из элементов отрицательный, поэтому при сложении этих чисел, необходимо подставлять модуль этого числа. Найдем их сумму: 3+2=5. В третьей строке стоят элементы 8, и -8. Один из элементов отрицательный, поэтому при сложении этих чисел, необходимо подставлять модуль этого числа. Найдем их сумму: 8+8=16. Максимальное из этих трех чисел - это 16. Значит третья  норма матрицы равна 16.
Нормы матрицы

 

 

Составитель: Салий Н.А.

Яндекс.Метрика

МЕНЮ УРОКА:

  • Инструкционная карта
  • Лекция
  • Лабораторная работа
  • Контроль

    • СТУДЕНТУ:

  • ООП
  • ЧИСЛЕННЫЕ МЕТОДЫ
  • ОАиП
  • FLASH АНИМАЦИЯ
  • ВСТ

    • ПЕДАГОГУ:

  • МЕТОДИКА
  • СТАТЬИ
  • Календ.-тем.планирование
  • Планы уроков
    •

    Сайт преподавателя программирования

    Сайт создан в системе uCoz