• Главная»
• Численные методы»
• Лекции»
• Урок №8. Определитель, его свойства

Урок №8. Определитель, его свойства

Вычисление определителя ручным способом

Определителем матрицы первого порядка, или определителем первого порядка, называется элемент а11:

Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:

Определить количество слагаемых, для нахождения определителя матрицы, в алгебраической сумме, можно вычислив факториал:

Свойства определителей матриц
Свойство № 1: Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование). |А| = |А|Т
Свойство № 2: При перестановке 2-х строк или столбцов матрицы ее определитель изменит знак на противоположный, сохраняя абсолютную величину.

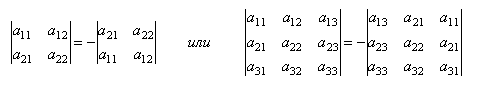
Свойство № 3: Определитель матрицы, имеющий два одинаковых ряда, равен нулю.

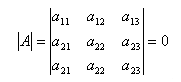
Свойство № 4: Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя.

Следствия из свойств № 3 и № 4: Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой определитель матрицы равен нулю.
Свойство № 5: Если все элементы какой–либо строки или столбца определителя матрицы равны нулю, то сам определитель матрицы равен нулю.
Свойство № 6: Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель матрицы можно представить в виде суммы 2-х определителей по формуле:

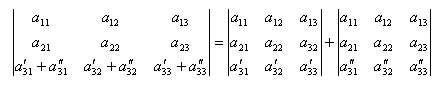
Свойство № 7: Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель матрицы не изменит своей величины.

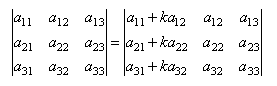
Пример 1. Вычислить определитель произведения матриц A и B.

Вычисление определителя с помощью Excel
В Excel для вычисления определителя квадратной матрицы используется функция МОПРЕД. Функция имеет вид
МОПРЕД(массив).
Здесь массив – это числовой массив, в котором хранится квадратная матрица. При этом массив может быть задан как интервал ячеек, например, A1:C3, или как массив констант, например, {1;2;3: 4;5;6: 7;8;9}.

Пример 2. Найти определитель матрицы .

Ход решения:

1. Введите матрицу (рис.1)

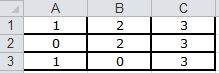
Рисунок 1. Матрица А

1. Курсор поставьте в ячейку, в которой необходимо получить значение определителя, например в A4.
2. Вызовите Мастер функции и в категории «Полный алфавитный перечень» найдите функцию МОПРЕД. После этого щелкните ОК.
3. В появившемся окне укажите диапазон (A1:C3), в котором находится матрица, и нажмите ОК.
4. В результате в ячейке появится значение определителя матрицы = 6.

Задание 1:  вычислить с помощью Excel определитель из примера 1.
Задание 2:  вычислить с помощью Excel определитель из семестрового задания по своему варианту.

 

 

 

Составитель: Салий Н.А.